얘는 대체 왜 이럴까? (모르면 죽을 수 있음)

초등학교 저학년도 알 것 같은 문제를 틀리는 컴퓨터씨...

0.1 + 1.1은 1.2가 아니란다. 컴퓨터 이녀석 정확한 놈인 줄 알았는데 마냥 그렇지도 않은가보다.

메모리

저 값들은 메모리에 쓰여지는 값들이다. 메모리가 어떻게 생겼는 지 이해할 필요가 있다.

메모리 구조

메모리는 0과 1을 저장할 수 있는 bit라고 부르는 칸이 무수히 많이 뭉쳐진 구조이다. 여기엔 0과 1만 저장할 수 있기 때문에 컴퓨터가 데이터를 저장하는 방법에 따라서 공간을 잡고 데이터를 저장한다.

ex)

• 정수 5 → 00000101
• 정수 10 → 00001010
• 더 큰 수를 저장하고 싶으면 칸을 늘려서 저장 16칸은 -32768 ~ 32767까지 저장 가능

 

실수형은 어떻게 저장할까? (float 자료형 기준)

5.125라는 숫자를 저장하려면 어떻게 할까? 5.125 → 101.001(2진법)

컴퓨터는 실수를 저장하기 위해 다음과 같은 방법을 사용한다고 한다.

1. 일단 메모리에 숫자를 저장하기 위한 칸을 넉넉히 32칸정도 잡는다.
2. 맨 첫번째 칸엔 숫자의 부호를 저장한다. (양수는 0, 음수는 1)
3. 그다음 실수의 소수점을 맨 왼쪽으로 이동한 다음 101.001 → 1.01001 * 2²
4. 여기서 지수 부분(2)에 127을 더한 다음에 이진법으로 앞에 8자리에 넣는다. 1000 0001
5. 그리고 소수 부분은 맨 뒤에 23칸에 밀어 넣는다. 01001

5.125를 메모리에 저장할 때

 

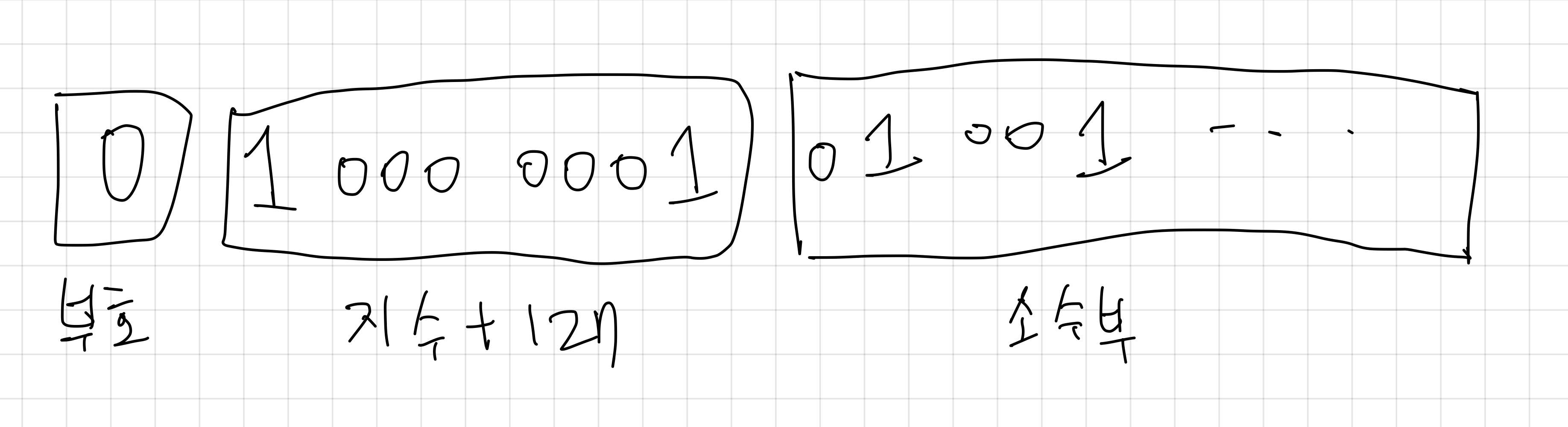
순환 소수🤪

0.125같은 숫자는 2진수로 0.001 처럼 딱 나누어 떨어진다. 근데 0.1같은 숫자는 2진수로 어떻게 표시되나?

소수를 이진수로 변환하는 법은 결과가 1로 나누어 떨어질 때까지 2를 곱하면서 정수부를 뽑으면 된다.

0.1을 가지고 해볼까?

000110011001100110011001100110011………

반복 패턴이 생겼고 순환소수가 돼버렸다…

이걸 float 변수에 저장하면 어떻게 저장될까? 저장 가능한 칸까지만 저장하고 뒷 부분은 그냥 잘라버린다. 왜냐면 세상에 무한히 반복되는 숫자를 저장할 수 있는 저장공간은 없으니까.

근데 그러면 자른 부분만큼 오차가 발생하게 된다.

즉 0.1처럼 이진수로 변환할 때 순환소수가 되는 값은 애초에 컴퓨터에 담을 수 없는 값이었다.

 

이거 모르면 죽음

이런거 모르고 코드를 짜면 죽을 수가 있다. 장난이 아니고 진짜로 죽는다.

패트리어트 미사일의 실패

실제로 걸프전때 패트리어트라는 미사일 요격 장비가 있었다. 이 장비를 구동시키는 프로그램이 있었는데 그 프로그램에서 시간을 측정하는데 시간을 0.1초 단위로 측정을 했다. 변수같은거 만들어 두고 거기다 0.1씩 더하는 방식으로…

0.1초마다 시간을 더하는 애

근데 이 프로그램에선 실수형 자료의 저장 공간으로 24칸을 사용했다고 한다. 그러다 보니 1시간마다 약 0.0034초의 오차가 발생했다.

어느날 이 프로그램을 100시간동안 연속으로 돌려놨는데… 약 0.34초의 오차가 발생했고, 그 오차때문에 날아오는 미사일의 좌표 계산을 실패해서 요격에 실패해서 28명이 전사했단다.

 

그럼 저런 숫자를 쓰고싶으면 어떻게 해야해?

그렇게 정확성이 필요하지 않은 값이라면 실수형을 사용해도 된다. 근데 정말 정확한 계산이 필요한 데이터라면..? ex) 돈… 돈… 돈..

1. 정말 정확한 계산이 필요하다면 정수형으로 바꿔서 저장해라. ex) 5.1달러 → 5100센트
2. 꼭 엄청 정확할 필요는 없는데, 오차를 줄이고 싶다면 double 자료형을 쓰면 된다. float보다 두배의 칸을 사용하기 때문에 오차가 매우매우 작아진다. 단점은 float보다 메모리 용량을 두배 먹는다는 정도..?

Ref

https://www.youtube.com/watch?v=-GsrYvZoAdA

http://www-users.math.umn.edu/~arnold//disasters/patriot.html